Os estudos da Geometria Plana tiveram início na Grécia Antiga, e pode ser chamada também de Geometria Euclidiana, por causa de Euclides de Alexandria (360 a.C. – 295 a.C.). Este matemático frequentou a escola baseada nos princípios de Platão e foi educado na cidade de Atenas. Os princípios da Geometria Plana eram baseados nos estudos do ponto, da reta e do plano. O ponto era considerado um elemento que não tinha definição, a reta era definida como uma sequência infinita de pontos e o plano definido através da disposição de retas.

Podemos destacar a Geometria Plana também como o estudo de matérias que não possuem volume, ao contrário da Geometria Espacial, que estuda as matérias com volumes sólidos, figuras com três dimensões, como os cones, cubos, cilindros, prismas, pirâmides e esferas.

Geometria Euclidiana

A base da Geometria Euclidiana se manteve por cerca de dois milênios, até que, no século XIX, contrariando um dos postulados de Euclides, o russo Nicolai Lobatchevski, húngaro Farkas Bolyai e o alemão Karl Gauss desenvolveram independentemente a geometria hiperbólica, enquanto Riemann elaborou a geometria elíptica.

Segundo os postulados de Euclides, por um ponto fora de uma reta pode ser traçada uma única reta paralela à primeira. Na geometria hiperbólica, por um ponto exterior a uma reta passam infinitas retas paralelas a ela. Mas os outros postulados da geometria euclidiana são conservados.

Na geometria desenvolvida por Riemann, as linhas retas são curvas finitas fechadas. Essa geometria é constituída sobre superfícies esférica. As linhas retas são os círculos máximos da esfera.

Conceitos básicos

Pontos: Os pontos são representados por letras maiúsculas (A, B, C), as retas são representadas por letras minúsculas (r, s, t) e os planos com letras do alfabeto grego (α, β, γ). E quando dois pontos definem uma reta, pode-se indicar a reta por dois de seus pontos.

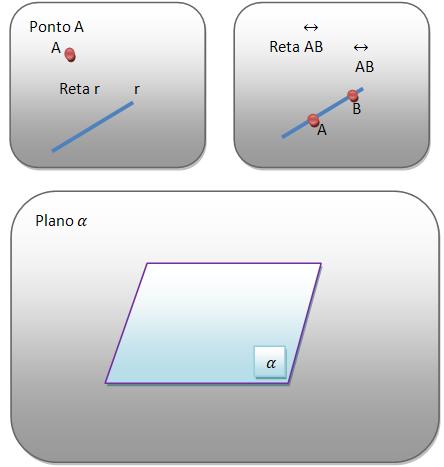
Exemplos de ponto, reta e plano

Reta: As retas são linhas ilimitadas que possuem infinitos pontos. Elas podem ser horizontais, verticais e inclinadas. A relação entre duas retas também pode ser determinada, como retas concorrentes (as que se cruzam), paralelas (estão na mesma direção e nunca se encontram), perpendiculares (formam um ângulo de 90º), etc. A reta é representada por uma letra.

Segmento de reta: A reta em si é uma linha ilimitada, como dito, que possui infinitos pontos dentro de si. Um segmento de reta é um “pedaço” da reta, delimitado por dois pontos. O segmento de reta é representado por duas letras, que determinam os pontos limites, como AB.

Plano: O plano é dimensionado pela largura e comprimento, possui diversas retas e diversos pontos dentro de si. É representado por letras gregas, como foi mostrado na imagem acima.

Ângulo: O ângulo é ocasionado pelo encontro de duas retas. Por exemplo, quando retas perpendiculares se cruzam, elas formam um ângulo de 90º. Porém, elas podem ser apenas concorrentes e formar ângulos agudos, menores que 90º, ou ângulos obtusos, maiores que 90º.

Área: A área é uma medida que resulta da multiplicação da largura do plano pelo seu comprimento. Ela expressa o tamanho de uma superfície.

Perímetro: O perímetro é uma medida que soma os lados de um plano. Assim, saberá o comprimento total dos lados.

Figuras Geométricas

Outra área de estudo da Geometria Plana são as figuras geométricas planas. Temos como exemplo os triângulos. É muito importante o estudo dos triângulos, área chamada de trigonometria, pois ela é responsável por grande parte dos cálculos de áreas e fazem parte também de muitas questões do Enem.

Os triângulos podem ser classificados de acordo com os seus lados.

• Triângulo Equilátero: tem os três lados iguais.
• Triângulo Isósceles: tem dois lados iguais e um diferente.
• Triângulo Escaleno: tem os três lados diferentes.

Ou podem também ser classificados de acordo com seus ângulos.

• Retângulo: quando possui um ângulo reto.
•  Acutângulo: quando possui os três ângulos agudos.
• Obtusângulo: quando possui um ângulo obtuso.

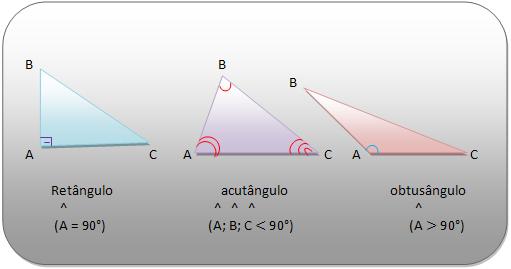
Classificação quanto aos ângulos

Observações:

• Todo triângulo isósceles pode ser chamado também de isoângulo.
• Todo triângulo equilátero pode ser chamado também de equiângulo, onde seus ângulos também são iguais, como seus lados. e cada ângulo mede 60°.
• A soma dos ângulos de um triângulo sempre é igual a 120°.
• O lado oposto ao ângulo reto de um triângulo retângulo é denominado hipotenusa, onde os outros dois lados são denominados catetos.

Outra figura geométrica estudada é o quadrado. Como pode-se ver abaixo, ele possui todos os lados de medida igual, e os ângulos são de 90º. A reta “d” presente, cortando a figura ao meio, é a diagonal.

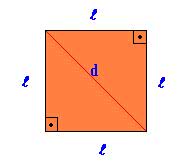
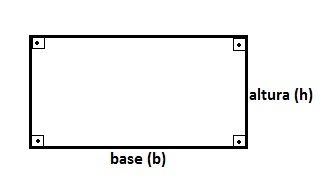
Abaixo, vemos o retângulo. É uma figura plana que possui dois lados iguais, paralelos horizontais, e dois lados iguais paralelos verticais. Todos os lados do retângulo também formam um ângulo reto de 90º.

Existem diversas outras formas geométricas que são parte da geometria plana, como a circunferência, pentágono, hexágono, losango, paralelogramo, etc. A característica comum a todas estas figuras é que elas não possuem volume, são bidimensionais.