Em matemática, a função polinomial é uma função dada por um polinômio. Chamamos de função polinomial do 1º grau a função f: R ➙ R, sendo f(x) = ax + b com a, b pertencentes a R e a diferente de 0. Esta função também pode ser chamada de função afim.

Veja alguns exemplos de Função Polinomial de 1º Grau:

• f(x) = 3x – 4, onde a = 3 e b = -4;
• f(x) = 5x, onde a = 5 e b = 0;
• f(x) = 11x, onde a = 11 e b = 0.

Características importantes

• Conjunto domínio: conjunto dos números reais, sendo D(f) = R;
• Conjunto imagem: conjunto dos números reais, sendo Im(f) = R;
• Coeficiente angular: o coeficiente de a;
• Coeficiente linear: o coeficiente de b;
• As funções de 1º grau podem ser crescentes, quando a > 0 e decrescentes, quando a < 0.

Exemplos:

• Na função f(x) = 2x + 7:
  • Coeficiente angular = 2
  • Coeficiente linear = 7
  • A função é crescente, pois 2 é maior que 0.

Casos particulares

Exemplo de Gráfico da Função Polinomial

Função linear: a função pode ser chamada de linear quando o coeficiente de b for nulo, ou seja, b = 0, sendo f(x) = ax

Exemplos:

• y = 3x
• y = x

Função identidade: ocorre nos casos em que o termo b = 0 e a = 1, tendo como forma f(x) = x.

Nota: caso o termo a seja nulo (a = 0) a função não é de primeiro grau e passa a ser chamada de função constante, tendo como forma f(x) = b.

O Gráfico

O gráfico de uma função polinomial do 1º grau,  y = ax + b, com a diferente de 0, é uma reta oblíqua aos eixos Ox e Oy. Veja o exemplo abaixo:

•  y = 3x – 1: Vamos construir o gráfico dessa função. Como o gráfico é uma reta, basta obter dois de seus pontos e ligá-los com o auxílio de uma régua:

a)    Para   x = 0, temos   y = 3 · 0 – 1 = -1; portanto, um ponto é (0, -1).
b)    Para   y = 0, temos   0 = 3x – 1; portanto, e outro ponto é .

Marcamos os pontos (0, -1) e no plano cartesiano e ligamos os dois com uma reta.

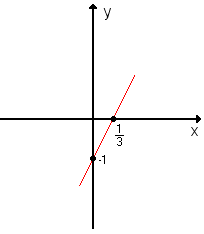
Então podemos dizer que o gráfico da função afim y = ax + b é uma reta.