Já imaginou a sua vida sem os números? Nem dá pra pensar, não é mesmo?! Os  números são muito importantes em nossas vidas, não somente na matemática, mas em diversas áreas de estudos. E para iniciar os estudos da matemática, é necessário conhecer os conjuntos numéricos, base da matemática.

Os números são divididos em diversas categorias, sendo que cada uma possui características próprias e juntas formam um conjunto numérico específico. Vamos falar um pouco sobre cada um desses conjuntos numéricos e suas características.

Os conjuntos numericos podem ser divididos em:

Conjunto dos números naturais (N)

Esse conjunto é formado por todos os números inteiros e positivos, incluindo o zero. É infinito e ilimitado. O conjunto dos números naturais sempre é representado pela letra N maiúscula. Para representar o conjunto dos números naturais não nulos, excluindo o zero, deve-se colocar um * na frente do N.

Exemplo:

N = {0, 1, 2, 3, 4, 5, 6, …}

N* = {1, 2, 3, 4, 5, 6, …}

Conjunto dos números inteiros (Z)

É a união dos números naturais (N) com os números inteiros negativos. Também é infinito e ilimitado. É representado pela letra Z maiúscula.

Exemplo:

Z = {…, -4, -3, -2, -1, 0, 1, 2, 3, 4, …}

O conjunto dos números inteiros (Z) tem algumas subdivisões:

Inteiros não negativos

Nesse subconjunto, os números negativos são excluídos, ficando apenas os números positivos e o zero. Logo, podemos observar que este conjunto é igual ao conjunto dos números naturais (N). É representado por Z₊:

Z₊ = {0, 1, 2, 3, 4, 5, 6, …}

Inteiros não positivos

São todos os números inteiros que não são positivos. É representado por Z_–:

Z_– = {…, -5, -4, -3, -2, -1, 0}

Inteiros não negativos e não-nulos

É o conjunto Z₊ excluindo o zero. Representa-se esse subconjunto por Z*₊:

Z*₊ = {1, 2, 3, 4, 5, 6, 7, …}

Observe que o conjunto Z*₊ = N*.

Inteiros não positivos e não nulos

Nesse subconjunto estão todos os números do conjunto Z_– excluindo o zero. Representa-se por Z*_–.

Z*_– = {… -4, -3, -2, -1}

Conjunto dos números racionais (Q)

É composto por números que podem ser representados em forma de fração, sempre com numerador e denominador pertencentes a Z. É um conjunto infinito e ilimitado. É representado pela letra Q maiúscula.

Exemplo:

Q = {½, ¾}

Dízima periódica

Quando uma fração não é equivalente a uma fração decimal exata, sua representação decimal passa a ser o que chamamos de dízima periódica. Na dízima periódica chamamos a parte da fração que se repete de período infinitamente.

Exemplo: 0,7878787878… , onde 78 é o período.

Conjunto dos números irracionais (I)

São aqueles que são decimais infinitos, mas não são periódicos. Um bom exemplo de número irracional é o número PI (resultado da divisão do perímetro de uma circunferência pelo seu diâmetro), que vale 3,14159265 … É representado pela letra I maiúscula.

Exemplo:

Π (Pi) = 3,141592…

Repare que os números são infinitos, mas não são periódicos.

Conjunto dos números reais (R)

É a união dos números racionais e irracionais, ou seja, todos os números citados acima. Esse conjunto é representado pela letra R maiúscula.

O diagrama abaixo mostra que cada conjunto é uma ampliação do anterior, sendo parte dele e acrescentando outros números:

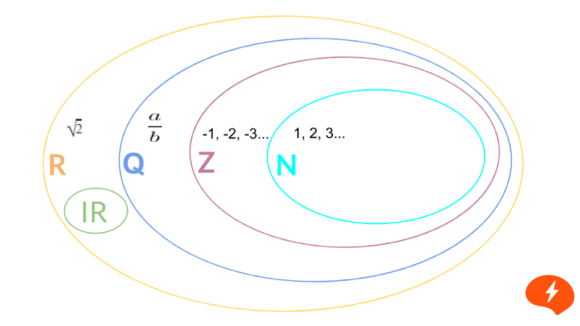
Representação dos conjuntos numéricos